Arquivo de etiquetas: identidade

Álgebra Abstracta, Matemática, Teoria de Grupos, Teoria de Representação de Grupos

Teoria de Representações de Grupos (Post #2)

1 comentário

É preciso começar pelo início. Duas questões se poêm: se a Teoria de Representação estabelece um meio de determinar representações de um grupo, o que significa exactamente um grupo ou uma representação?

A pergunta é inocente mas necessária. De um modo geral, uma maneira saudável de visualizar o problema seria: “Dado um grupo de rotações – um conjunto de rotações e transformações de elementos, que mapas posso eu criar que mantenham a estrutura do grupo num contexto de matrizes?  É aqui que reside a parte computacional da Teoria: a utilidade máxima é de representar grupos, normalmente como transformações, simetrias, através de uma certa álgebra noutro espaço. Neste caso, o espaço escolhido é o espaço de todos os operadores lineares de um espaço vectorial, como vamos ter a oportunidade de ver.

Um espaço vectorial – a ideia

Uma das maneiras mais simples de criar um sistema algébrico é através de operações simples: nomeadamente a adição e a multiplicação. No entanto, definir multiplicação de objectos não é uma operação consensual. Muitas imposições podem ser impostas: pensa como é diferente a ideia de multiplicação entre números, vectores  e matrizes ou mesmo de tensores; até multiplicação de conjuntos pode ser definida. Estas operações variam muito na definição e então multiplicação não é então uma operação desejada. Uma subsiste no entanto: o conceito de escalonamento de um objecto é algo relativamente bem definido: pegando num objecto, temos a noção que podemos multiplicar o mesmo por um factor que o mantenha fixo, se torne maior ou menor. O conceito de linearidade nasce destes dois conceitos básicos. Daqui, o espaço de todos os vectores resultantes destas operações é criado – chama-se um espaço vectorial.

Definição 1: (Espaço Vectorial)

Seja V um conjunto de elementos. Um espaço vectorial (V,+, \cdot) sobre um corpo \mathbb{F} é um triplo em que + : V \times V \rightarrow V and \cdot : \mathbb{F} \times V \rightarrow V são operação binárias tal que \forall x,y,z \in V

  1. x+y = y+x (Comutatividade da Adição)
  2. x+(y+z) = (x+y)+z (Associatividade da Adição
  3. \exists 0 \in V tal que x+0 = 0+x = x (Existência de uma identidade aditiva)
  4. \forall x \in V, \exists -x \in V tal que x+(-x) = (-x)+x = 0 (Existência de uma inversa aditiva)
  5. \forall \alpha \in \mathbb{F}, \alpha ( x+y) = \alpha x + \alpha y (Distributividade da multiplicação escalar com respeito à adição)
  6. \forall \alpha \ \beta \in \mathbb{F}, (\alpha + \beta)x = \alpha x + \beta x (Distributividade da muliplicação escalar com respeito à adição do corpo (1))
  7. \forall \alpha, \ \beta \in \mathbb{F}, \alpha ( \beta x) = (\alpha \beta) x (Compatibilidade da multiplicação escalar com a multiplicação do corpo (2))
  8. \exists 1 \in \mathbb{F} tal que 1x = x (Existência de uma identidade multiplicativa escalar)

Porquê “sobre um corpo 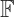\mathbb{F}

É necessário ler, uma por uma, as propriedades e entender o que é permitido fazer possível num espaço vectorial. Não muito: adicionar elementos e multiplicá-los por escalares; mas o que é um escalar, neste contexto?

Os “números” que “escalonam”  um dado elemento são chamados de “escalares” e são constantes. O conjunto escolhido podia ser aleatório no entanto escolheu-se um tipo muito específico: um corpo. Relembra-te o que é um corpo neste post. A justificação é muito básica:

  • Somar qualquer múltiplo de um elemento é sempre bem definido, pois a soma dos escalares está de novo no conjunto inicial.
  • Para qualquer soma há sempre uma “subtracção” tal que o resultado seja revertido ao início. O mesmo se aplica a múltiplos de elementos.
  • Para qualquer múltiplo de um múltiplo, o múltiplo final está de novo no conjunto e então é bem definido – axioma 7.
  • A existência de elementos “neutros” para a multiplicação e adição de vectores.

Embora a teoria seja geral e se inclua qualquer corpo \mathbb{F}, os mais comuns são os números reais \mathbb{R} e os complexos \mathbb{C}. O espaço vectorial é então denotado por real ou complexo, respectivamente.

Exemplos

O melhor exemplo é dado pela motivação da definição: um conjunto feito de vectores no plano ou no espaço. Adicionar é definido pela “regra do triângulo” e a multiplicação escalar como o alongamento ou retracção do comprimento do vector, mantendo a mesma direcção.

Adição de vectores no plano
O método é bastante semelhante à Regra do Paralelogramo, mas agora toma-se o segundo vector por \vec{-B}
Repara no vector original \vec{A}. A operação que se pretende definir é uma tal que a direcção original do vector seja mantida mas que o seu sentido e comprimento possam mudar. Para o vector do meio, após multiplicação pelo escalar -2 o seu sentido mudou (por causa do sinal negativo) e o seu comprimento duplicou (por causa do 2). Já no terceiro, o escalar \frac{1}{2} diminuiu o vector para metade do seu comprimento inicial, mantendo o sentido.

Mais exemplos podem ser dados. Exemplos mais sofisticados incluem um conjunto de funções contínuas num intervalo fechado. A adição é definida como (f+g)(x) = f(x) + g(x), para x no intervalo e (\alpha f )(x) = \alpha f(x).Agora que sabemos o que é um espaço vectorial, temos ferramentas para estudar espaço vectorial importante: o de operadores lineares num espaço vectorial. Mais no próximo post!

___________
(1) A propriedade de que \mathbb{F} é um corpo faz com que \alpha + \beta \in \mathbb{F} \forall \alpha, \ \beta \in \mathbb{F}. É uma propriedade bem definida então.

(2) Pela mesma razão que (1), a multiplicação de elementos de um corpo é igualmente bem definida, pelos axiomas de corpos (a multiplicação é uma operação binária e portanto fechada)